DimensionalData.jl

Named dimensions for julia data

Rafael Schouten
rafaelschouten@gmail.com

Globe Intstitute, Copenhagen University

2024-07-10

Why another named array package?

  • Geospatial data:
    • named dimensions and lookup values are ubiquitous
    • selecting spatial and temporal subsets is ubiquitous
    • there are a lot of possible lookup configurations
    • multi-array datasets are also common

  • xarray

Concepts: Dimensions

Dimension are wrappers


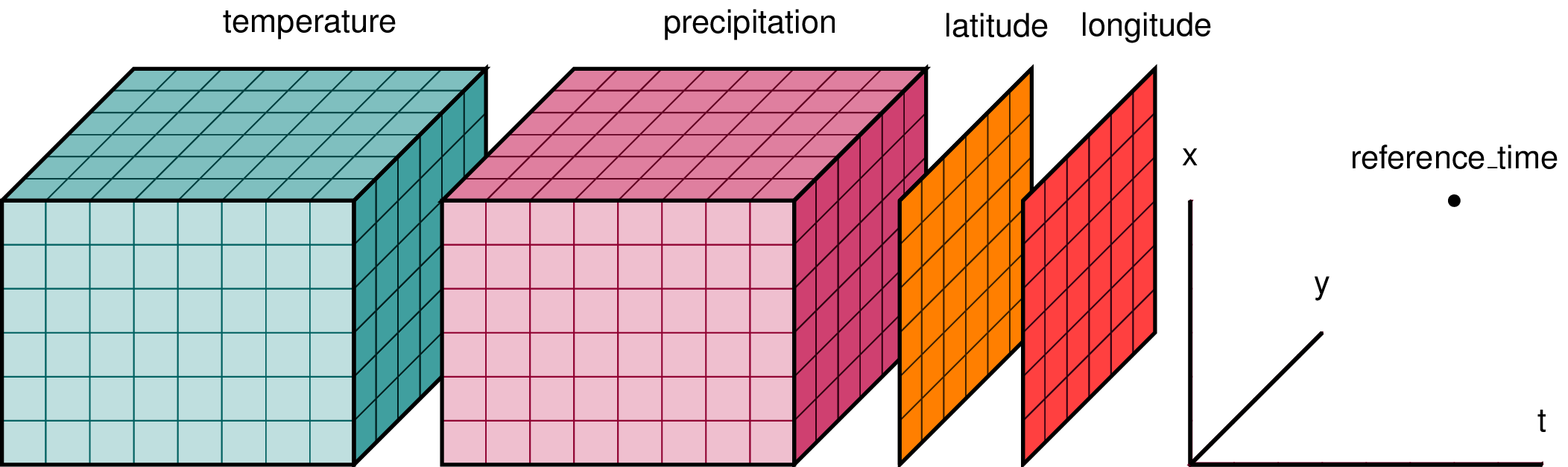
They mark that the wrapped object belongs to the dimension:

An integer:

X(1)
X 1

A range:

X(50:10:100)
X 50:10:100

A selector :

X(Not(At(70)))
X InvertedIndices.InvertedIndex{At{Int64, Nothing, Nothing}}(At(70, nothing, nothing))


“Standard” dimensions (90% of spatial data):

X, Y, Z, Ti
(X, Y, Z, Ti)

Arbitrary dimensions (everything else)

Dim{:name}
Dim{:name}

Lookups

  • Hold lookup values along a dimension
  • And traits like Points or Intervals
  • mostly detected automatically in array constructors

You can define them manually when you need to:

using DimensionalData.Lookups
l = Sampled(1:10; sampling=Intervals(Start()), order=ForwardOrdered(), span=Regular())
Sampled{Int64} ForwardOrdered Regular Intervals{Start}
wrapping: 1:10


Sampled <: AbstractSampled <: Aligned <: Lookup <: AbstractVector
false

DimArray Constructors

  • DimArray <: AbstractDimArray <: AbstractArray

1 dimensional


A = DimArray([1, 2, 3], X([:a, :b, :c]))
╭─────────────────────────────╮
│ 3-element DimArray{Int64,1} │
├─────────────────────────────┴───────────────── dims ┐
  ↓ X Categorical{Symbol} [:a, :b, :c] ForwardOrdered
└─────────────────────────────────────────────────────┘
 :a  1
 :b  2
 :c  3

N dimensional

With standard dimensions in a Tuple:

A = DimArray(rand(3, 4), (X([:a, :b, :c]), Y(10.0:10:40.0)))
╭─────────────────────────╮
│ 3×4 DimArray{Float64,2} │
├─────────────────────────┴─────────────────────────────────── dims ┐
  ↓ X Categorical{Symbol} [:a, :b, :c] ForwardOrdered,
  → Y Sampled{Float64} 10.0:10.0:40.0 ForwardOrdered Regular Points
└───────────────────────────────────────────────────────────────────┘
 ↓ →  10.0       20.0       30.0       40.0
  :a   0.342617   0.46755    0.324454   0.811161
  :b   0.17629    0.618897   0.23128    0.260502
  :c   0.452733   0.251785   0.85885    0.834195

With arbitrary Dim dimensions, in a NamedTuple:

DimArray(rand(3, 4), (a=[:a, :b, :c], b=10.0:10:40.0))
╭─────────────────────────╮
│ 3×4 DimArray{Float64,2} │
├─────────────────────────┴─────────────────────────────────── dims ┐
  ↓ a Categorical{Symbol} [:a, :b, :c] ForwardOrdered,
  → b Sampled{Float64} 10.0:10.0:40.0 ForwardOrdered Regular Points
└───────────────────────────────────────────────────────────────────┘
 ↓ →  10.0       20.0       30.0       40.0
  :a   0.670531   0.431686   0.930199   0.260112
  :b   0.518717   0.412699   0.776897   0.251387
  :c   0.517501   0.731436   0.64018    0.628815

Shorthands: rand, fill, zeros, ones

rand(X(6), Y(10:2:20))
╭─────────────────────────╮
│ 6×6 DimArray{Float64,2} │
├─────────────────────────┴────────────────────────── dims ┐
  ↓ X,
  → Y Sampled{Int64} 10:2:20 ForwardOrdered Regular Points
└──────────────────────────────────────────────────────────┘
 10         12          14         16         18          20
  0.718435   0.158657    0.808367   0.100717   0.816818    0.862287
  0.640028   0.0344655   0.995837   0.799657   0.542344    0.921293
  0.422047   0.065179    0.166129   0.296414   0.920396    0.856656
  0.352291   0.0740475   0.447463   0.587279   0.0916422   0.392502
  0.151813   0.948753    0.219828   0.272536   0.518881    0.456842
  0.276715   0.867893    0.173395   0.64557    0.905879    0.122918

DimStack Constructors

  • DimStack <: AbstractDimStack

Layers with the same dimensions


ds = X([:a, :b, :c]), Ti(10.0:10:40.0)
S = DimStack((layer1=rand(Float32, 3, 4), layer2=zeros(Bool, 3, 4)), ds)
╭──────────────╮
│ 3×4 DimStack │
├──────────────┴─────────────────────────────────────────────── dims ┐
  ↓ X  Categorical{Symbol} [:a, :b, :c] ForwardOrdered,
  → Ti Sampled{Float64} 10.0:10.0:40.0 ForwardOrdered Regular Points
├──────────────────────────────────────────────────────────── layers ┤
  :layer1 eltype: Float32 dims: X, Ti size: 3×4
  :layer2 eltype: Bool dims: X, Ti size: 3×4
└────────────────────────────────────────────────────────────────────┘

Layers with different dimensions:


x, ti = X([:a, :b, :c]), Ti(10.0:10:40.0)
DimStack((twodims=rand(Float32, x, ti), onedim=zeros(Bool, x)))
╭──────────────╮
│ 3×4 DimStack │
├──────────────┴─────────────────────────────────────────────── dims ┐
  ↓ X  Categorical{Symbol} [:a, :b, :c] ForwardOrdered,
  → Ti Sampled{Float64} 10.0:10.0:40.0 ForwardOrdered Regular Points
├──────────────────────────────────────────────────────────── layers ┤
  :twodims eltype: Float32 dims: X, Ti size: 3×4
  :onedim  eltype: Bool dims: X size: 3
└────────────────────────────────────────────────────────────────────┘

Named indexing

DimArray:

using BenchmarkTools
@btime $A[3, 4]        # Base Julia Array syntax
@btime $A[Y(4), X(3)]  # Dimension wrappers
@btime $A[Y=4, X=3]    # Keyword syntax
  2.785 ns (0 allocations: 0 bytes)
  2.785 ns (0 allocations: 0 bytes)
  3.095 ns (0 allocations: 0 bytes)
0.8341949897901655

DimStack:

@btime $S[Ti(4), X(3)] # Dimension wrappers
@btime $S[Ti=4, X=3]   # Keyword syntax
  3.195 ns (0 allocations: 0 bytes)
  3.406 ns (0 allocations: 0 bytes)
(layer1 = 0.54143864f0, layer2 = false)

Selectors

  • select data with lookup values

At


Find exact or approximate matches

A = DimArray([1, 2, 3, 4], (X([10.0, 20.0, 40.0, 80.0])))
A[X(At(80.0))]
4
A[X(At(80.09; atol=0.1))]
4

Near


Find the closest match

A[X(Near(85))]
4

Contains


Find the interval that contains a value

# Define a DimArray with Intervals lookup
using DimensionalData.Lookups
A = DimArray(100:100:9900, X(1.0:1.0:99.0; sampling=Intervals(Start())))
# Index with Contains
A[X(Contains(9.5))]
900

.. (an IntervalSets.jl Interval)


Select data inside an interval

A[X=9.5 .. 15]
╭─────────────────────────────╮
│ 5-element DimArray{Int64,1} │
├─────────────────────────────┴──────────────────────────────────────── dims ┐
  ↓ X Sampled{Float64} 10.0:1.0:14.0 ForwardOrdered Regular Intervals{Start}
└────────────────────────────────────────────────────────────────────────────┘
 10.0  1000
 11.0  1100
 12.0  1200
 13.0  1300
 14.0  1400

Where


Make dimensional queries

A[X=Where(isodd)]
╭──────────────────────────────╮
│ 50-element DimArray{Int64,1} │
├──────────────────────────────┴───────────────────────────────────────── dims ┐
  ↓ X Sampled{Float64} [1.0, 3.0, …, 97.0, 99.0] ForwardOrdered Irregular Intervals{Start}
└──────────────────────────────────────────────────────────────────────────────┘
  1.0   100
  3.0   300
  5.0   500
  7.0   700
  9.0   900
 11.0  1100
  ⋮    
 91.0  9100
 93.0  9300
 95.0  9500
 97.0  9700
 99.0  9900

Plotting

Plots.jl

using Plots
Plots.scatter(rand(X([:a, :b, :c, :d])))

Makie.jl

using CairoMakie, Distributions
Makie.heatmap(rand(Normal(), X(100:10:200), Y([:a, :b, :c])))

Integrations

  • DimensionalData uses all abstract types so its extensible
  • Just dims and rebuild methods let other array types work like a DimArray

Some packages building on DimensionalData.jl

Thanks


(And checkout the new docs by Lazaro Alonzo!)

Docs