Reprojection and resampling
What is resampling?
resample "re-samples" the data by interpolation and can also aggregate or disaggregate, changing the resolution. It always returns a Regular lookup (like a range), and is the most flexible of the resampling methods.
This uses GDAL's gdalwarp algorithm under the hood. You can call that via warp if you need more control, but generally resample is sufficient.
warp, contributions are welcome!
- Show how to use
warpto reproject a raster
Rasters.jl has a few other methods to change the lookups of a raster. These are:
reproject, which directly reprojects the lookup axes (but is only usable for specific cases, where the source and destination coordinate systems are both cylindrical, like the long-lat, Mercator, or Web-Mercator projections.) This is a lossless operation and keeps the data exactly the same - only the axes are changed.aggregateanddisaggregate, which change the resolution of the raster by merging (aggregate) or splitting (disaggregate) cells. They can't change cells fractionally, and can't change the projection or coordinate system.
Of all these methods, resample is the most flexible and powerful, and is what we will focus on here. It is, however, also the slowest. So if another method is applicable to your problem, you should consider it.
How resample works
resample uses GDAL's gdalwarp algorithm under the hood. This is a battle-tested algorithm and is generally pretty robust. However, it has the following limitations:
It always assumes cell-based sampling, instead of point-based sampling. This does mean that point-based rasters are converted to cell-based sampling.
It can only accept some primitive types for the input data, since that data is passed directly to a C library. Things like
RGBor user-defined types are not usually supported.
resample allows you to specify several methods, see some of them in the next section.
resolution, size and methods
Let's start by loading the necessary packages:
using Rasters, RasterDataSources, ArchGDAL
using DimensionalData
using DimensionalData.Lookups
using NaNStatistics
using CairoMakieras = Raster(WorldClim{BioClim}, 5)
ras_m = replace_missing(ras, missingval=NaN)┌ 2160×1080 Raster{Float64, 2} bio5 ┐
├───────────────────────────────────┴──────────────────────────────────── dims ┐
↓ X Projected{Float64} -180.0:0.16666666666666666:179.83333333333331 ForwardOrdered Regular Intervals{Start},
→ Y Projected{Float64} 89.83333333333333:-0.16666666666666666:-90.0 ReverseOrdered Regular Intervals{Start}
├──────────────────────────────────────────────────────────────────── metadata ┤
Metadata{Rasters.GDALsource} of Dict{String, Any} with 1 entry:
"filepath" => "./WorldClim/BioClim/wc2.1_10m_bio_5.tif"
├────────────────────────────────────────────────────────────────────── raster ┤
extent: Extent(X = (-180.0, 179.99999999999997), Y = (-90.0, 90.0))
missingval: NaN
crs: GEOGCS["WGS 84",DATUM["WGS_1984",SPHEROID["WGS 84",6378137,298.257223563,AUTHORITY["EPSG","7030"]],AUTHORITY["EPSG","6326"]],PRIMEM["Greenwich",0,AUTHORITY["EPSG","8901"]],UNIT["degree",0.0174532925199433,AUTHORITY["EPSG","9122"]],AXIS["Latitude",NORTH],AXIS["Longitude",EAST],AUTHORITY["EPSG","4326"]]
└──────────────────────────────────────────────────────────────────────────────┘
↓ → 89.8333 89.6667 89.5 … -89.6667 -89.8333 -90.0
-180.0 NaN NaN NaN -15.399 -13.805 -14.046
-179.833 NaN NaN NaN -15.9605 -14.607 -14.5545
⋮ ⋱ ⋮
179.5 NaN NaN NaN -18.2955 -16.7583 -16.72
179.667 NaN NaN NaN -18.2847 -16.7513 -16.72
179.833 NaN NaN NaN … -17.1478 -15.4243 -15.701resampling to a given size or res ≡ resolution providing a method is done with
julia> ras_sample = resample(ras_m; size=(1440, 720), method="average")┌ 1440×720 Raster{Float64, 2} bio5 ┐
├──────────────────────────────────┴───────────────────────────────────── dims ┐
↓ X Projected{Float64} -180.0:0.25:179.75 ForwardOrdered Regular Intervals{Start},
→ Y Projected{Float64} 89.75:-0.25:-90.0 ReverseOrdered Regular Intervals{Start}
├──────────────────────────────────────────────────────────────────── metadata ┤
Metadata{Rasters.GDALsource} of Dict{String, Any} with 1 entry:
"filepath" => "/vsimem/tmp"
├────────────────────────────────────────────────────────────────────── raster ┤
extent: Extent(X = (-180.0, 180.0), Y = (-90.0, 90.0))
missingval: NaN
crs: GEOGCS["WGS 84",DATUM["WGS_1984",SPHEROID["WGS 84",6378137,298.257223563,AUTHORITY["EPSG","7030"]],AUTHORITY["EPSG","6326"]],PRIMEM["Greenwich",0,AUTHORITY["EPSG","8901"]],UNIT["degree",0.0174532925199433,AUTHORITY["EPSG","9122"]],AXIS["Latitude",NORTH],AXIS["Longitude",EAST],AUTHORITY["EPSG","4326"]]
└──────────────────────────────────────────────────────────────────────────────┘
↓ → 89.75 89.5 89.25 89.0 … -89.5 -89.75 -90.0
-180.0 NaN NaN NaN NaN -15.7547 -15.0816 -14.1678
-179.75 NaN NaN NaN NaN -16.1382 -15.5151 -14.5793
⋮ ⋱ ⋮
179.25 NaN NaN NaN NaN -18.594 -17.7993 -16.7431
179.5 NaN NaN NaN NaN -18.4647 -17.7799 -16.732
179.75 NaN NaN NaN NaN … -17.6831 -16.9734 -15.9826other available methods to try: "mode", "max", "sum", "bilinear", "cubic", "cubicspline", "lanczos", "min", "med", "q1", "q3" and "near".
Let's consider a few more examples, with the following options:
methods = ["average", "mode", "max", "sum"]
sizes = [(2160, 1080), (1440, 720), (720, 360), (360, 180)]
resolutions = [0.16666666666666666, 0.25, 0.5, 1.0];method_sizes = [resample(ras_m; size=size, method=method) for method in methods for size in sizes]
with_theme(Rasters.theme_rasters()) do
colorrange = (nanminimum(ras_m), nanmaximum(ras_m))
hm=nothing
fig = Figure(; size = (1000, 600))
axs = [Axis(fig[i,j], title="size=$(size), method=:$(method)", titlefont=:regular)
for (i, method) in enumerate(methods) for (j, size) in enumerate(sizes)]
for (i, ax) in enumerate(axs)
hm = heatmap!(ax, method_sizes[i]; colorrange)
end
Colorbar(fig[:,end+1], hm)
hidedecorations!.(axs; grid=false)
rowgap!(fig.layout, 5)
colgap!(fig.layout, 10)
fig
end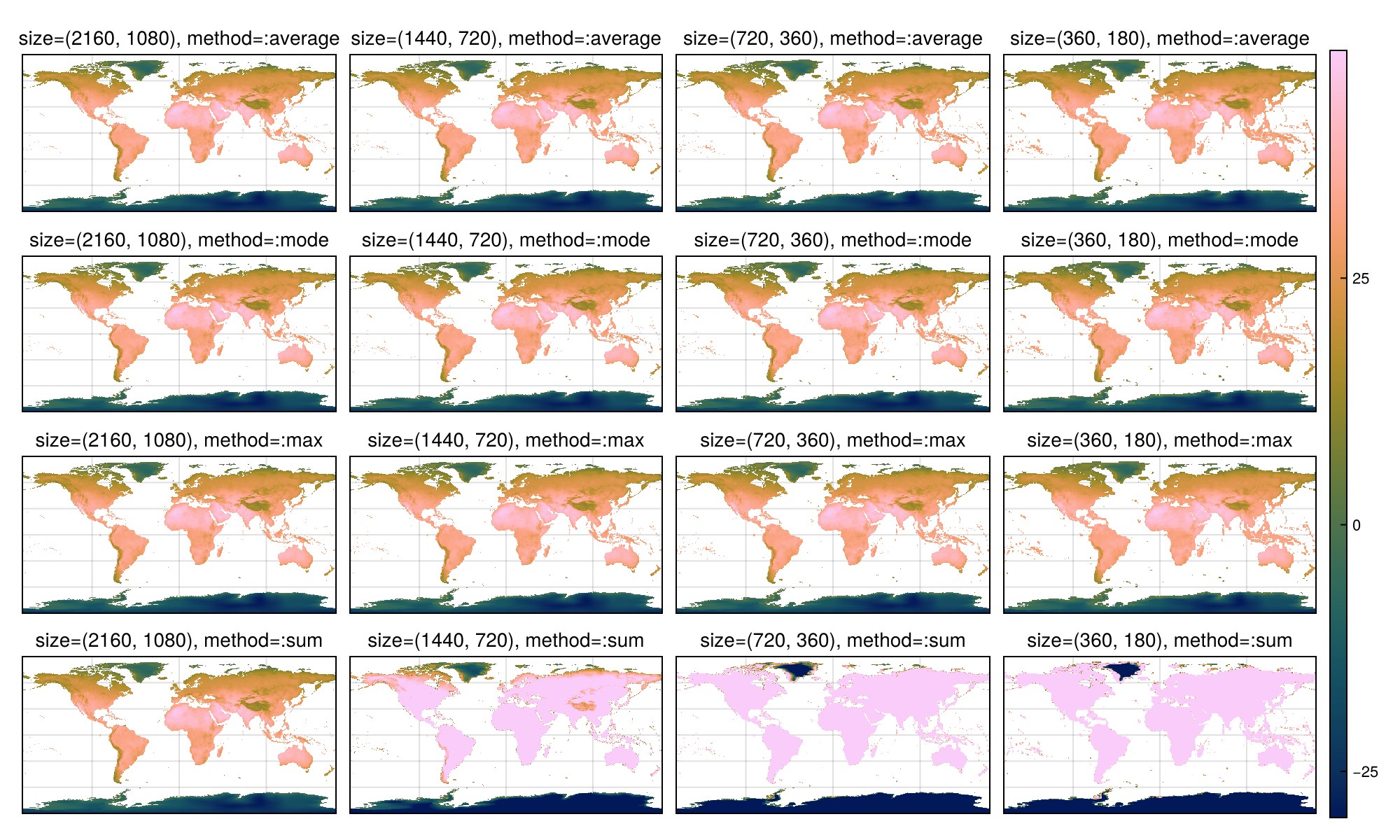
reproject with resample using a ProjString
Geospatial datasets will come in different projections or coordinate reference systems (CRS) for many reasons. Here, we will focus on MODIS SINUSOIDAL and EPSG, and transformations between them.
Let's load our test raster
ras = Raster(WorldClim{BioClim}, 5)
ras_m = replace_missing(ras, missingval=NaN);Sinusoidal Projection (MODIS)
SINUSOIDAL_CRS = ProjString("+proj=sinu +lon_0=0 +type=crs")ProjString: +proj=sinu +lon_0=0 +type=crsRaw MODIS ProjString
SINUSOIDAL_CRS = ProjString("+proj=sinu +lon_0=0 +x_0=0 +y_0=0 +a=6371007.181 +b=6371007.181 +units=m +no_defs")and the resample is performed with
ras_sin = resample(ras_m; size=(2160, 1080), crs=SINUSOIDAL_CRS, method="average")┌ 2160×1080 Raster{Float64, 2} bio5 ┐
├───────────────────────────────────┴──────────────────────────────────── dims ┐
↓ X Projected{Float64} -2.0037508342789244e7:18547.034693196307:2.000553955982158e7 ForwardOrdered Regular Intervals{Start},
→ Y Projected{Float64} 9.983453040980069e6:-18512.68833265335:-9.991737669952895e6 ReverseOrdered Regular Intervals{Start}
├──────────────────────────────────────────────────────────────────── metadata ┤
Metadata{Rasters.GDALsource} of Dict{String, Any} with 1 entry:
"filepath" => "/vsimem/tmp"
├────────────────────────────────────────────────────────────────────── raster ┤
extent: Extent(X = (-2.0037508342789244e7, 2.0024086594514776e7), Y = (-9.991737669952895e6, 1.0001965729312722e7))
missingval: NaN
crs: +proj=sinu +lon_0=0 +type=crs
└──────────────────────────────────────────────────────────────────────────────┘
↓ → 9.98345e6 9.96494e6 … -9.97322e6 -9.99174e6
-2.00375e7 NaN NaN NaN NaN
-2.0019e7 NaN NaN NaN NaN
⋮ ⋱ ⋮
1.99684e7 NaN NaN NaN NaN
1.9987e7 NaN NaN NaN NaN
2.00055e7 NaN NaN … NaN NaNTIP
GDAL always changes the locus to cell sampling, you can reset this by using shiftlocus.
let's compare the total counts!
nansum(ras_m), nansum(ras_sin)(1.1263161695036696e7, 1.1730134537265886e7)and, how does this looks like?
fig, ax, plt = heatmap(ras_sin)
Colorbar(fig[1,2], plt)
fig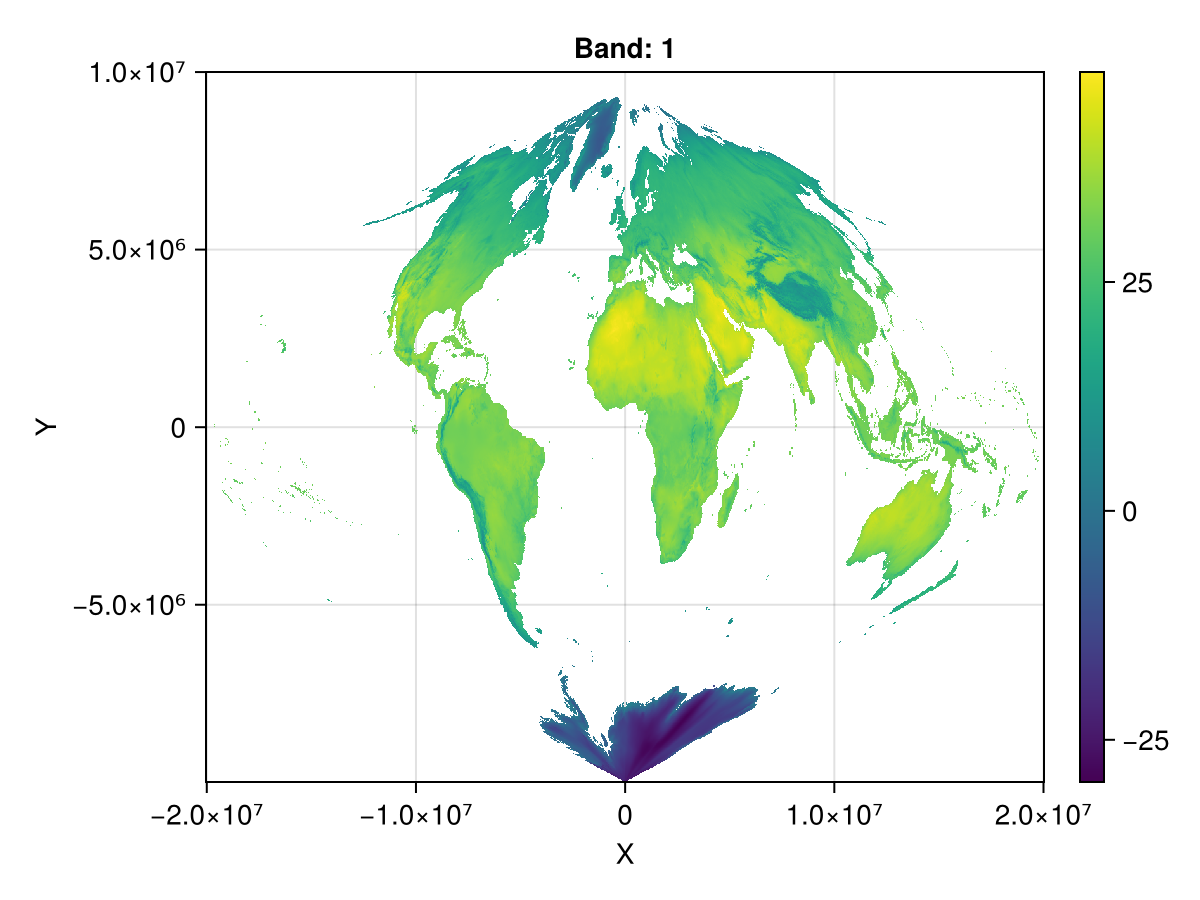
now, let's go back to latitude and longitude and reduce the resolution
ras_epsg = resample(ras_sin; size=(1440,720), crs=EPSG(4326), method="average")┌ 1440×720 Raster{Float64, 2} bio5 ┐
├──────────────────────────────────┴───────────────────────────────────── dims ┐
↓ X Projected{Float64} -180.0:0.25:179.75 ForwardOrdered Regular Intervals{Start},
→ Y Projected{Float64} 89.75002543153558:-0.2499745684644309:-89.98168929439024 ReverseOrdered Regular Intervals{Start}
├──────────────────────────────────────────────────────────────────── metadata ┤
Metadata{Rasters.GDALsource} of Dict{String, Any} with 1 entry:
"filepath" => "/vsimem/tmp"
├────────────────────────────────────────────────────────────────────── raster ┤
extent: Extent(X = (-180.0, 180.0), Y = (-89.98168929439024, 90.0))
missingval: NaN
crs: EPSG:4326
└──────────────────────────────────────────────────────────────────────────────┘
↓ → 89.75 89.5001 89.2501 … -89.4817 -89.7317 -89.9817
-180.0 NaN NaN NaN -22.341 -21.57 -21.7346
-179.75 NaN NaN NaN -22.3399 -21.5718 -21.7351
⋮ ⋱ ⋮
179.25 NaN NaN NaN -24.3415 -23.9049 -23.734
179.5 NaN NaN NaN -24.341 -23.9056 -23.7339
179.75 NaN NaN NaN … -24.3405 -23.9063 -23.7338and let's apply shiftlocus such that the lookups share the exact same grid, which might be needed when building bigger datasets:
locus_resampled = DimensionalData.shiftlocus(Center(), ras_epsg)┌ 1440×720 Raster{Float64, 2} bio5 ┐
├──────────────────────────────────┴───────────────────────────────────── dims ┐
↓ X Projected{Float64} -179.875:0.25:179.875 ForwardOrdered Regular Intervals{Center},
→ Y Projected{Float64} 89.8750127157678:-0.2499745684644309:-89.85670201015802 ReverseOrdered Regular Intervals{Center}
├──────────────────────────────────────────────────────────────────── metadata ┤
Metadata{Rasters.GDALsource} of Dict{String, Any} with 1 entry:
"filepath" => "/vsimem/tmp"
├────────────────────────────────────────────────────────────────────── raster ┤
extent: Extent(X = (-180.0, 180.0), Y = (-89.98168929439024, 90.00000000000001))
missingval: NaN
crs: EPSG:4326
└──────────────────────────────────────────────────────────────────────────────┘
↓ → 89.875 89.625 89.3751 … -89.3568 -89.6067 -89.8567
-179.875 NaN NaN NaN -22.341 -21.57 -21.7346
-179.625 NaN NaN NaN -22.3399 -21.5718 -21.7351
⋮ ⋱ ⋮
179.375 NaN NaN NaN -24.3415 -23.9049 -23.734
179.625 NaN NaN NaN -24.341 -23.9056 -23.7339
179.875 NaN NaN NaN … -24.3405 -23.9063 -23.7338Things to keep in mind
You can in fact resample to another raster
resample(ras; to=ref_ras), if you want perfect alignment. Contributions are welcome for this use case!This doesn't work for irregularly sampled rasters.
fig, ax, plt = heatmap(ras_epsg)
Colorbar(fig[1,2], plt)
fig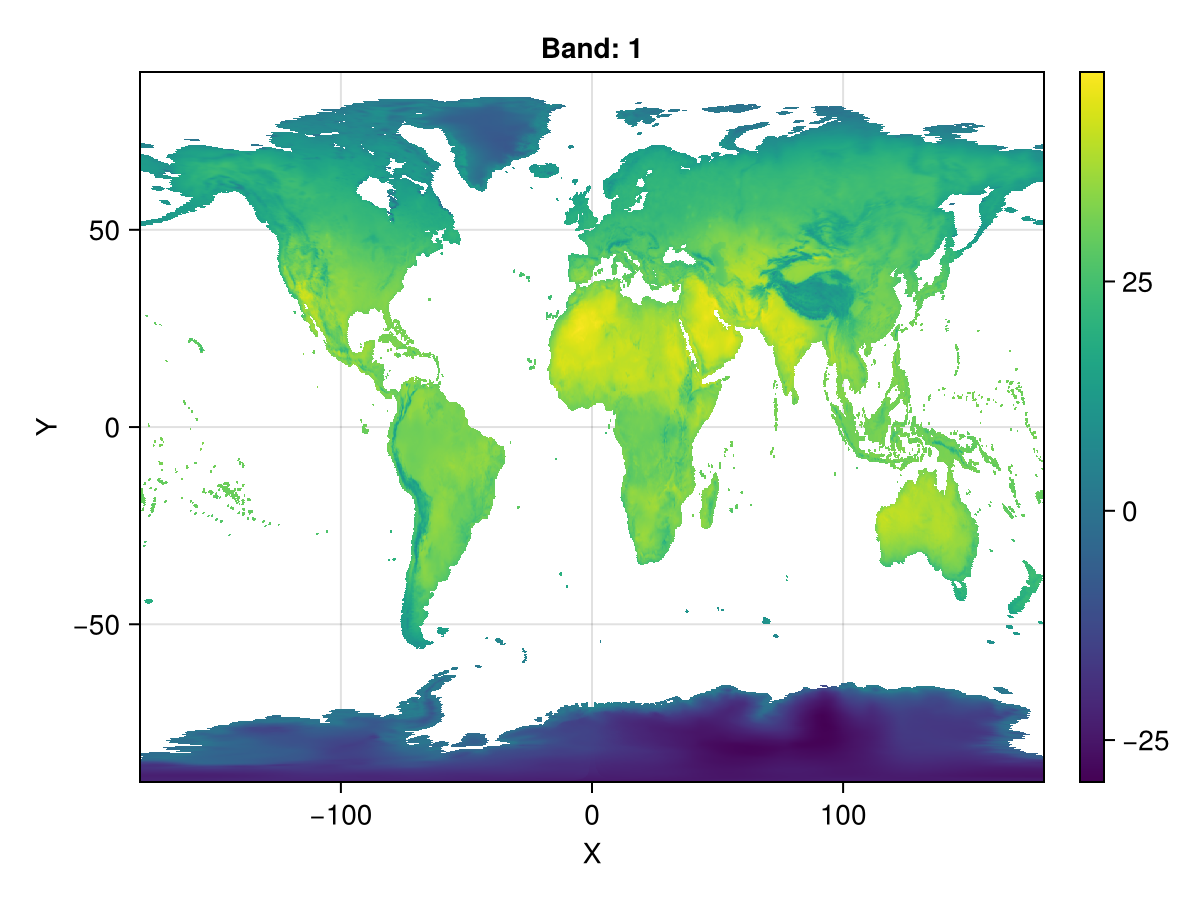
A Raster from scratch
x_range = LinRange(-180, 179.75, 1440)
y_range = LinRange(89.75, -90, 720)
ras_data = ras_epsg.datacreate the raster
julia> using Rasters.Lookups
julia> ras_scratch = Raster(ras_data, (X(x_range; sampling=Intervals(Start())),
Y(y_range; sampling=Intervals(Start()))), crs=EPSG(4326), missingval=NaN)┌ 1440×720 Raster{Float64, 2} ┐
├─────────────────────────────┴────────────────────────────────────────── dims ┐
↓ X Projected{Float64} LinRange{Float64}(-180.0, 179.75, 1440) ForwardOrdered Regular Intervals{Start},
→ Y Projected{Float64} LinRange{Float64}(89.75, -90.0, 720) ReverseOrdered Regular Intervals{Start}
├────────────────────────────────────────────────────────────────────── raster ┤
extent: Extent(X = (-180.0, 180.0), Y = (-90.0, 90.0))
missingval: NaN
crs: EPSG:4326
└──────────────────────────────────────────────────────────────────────────────┘
↓ → 89.75 89.5 89.25 89.0 … -89.5 -89.75 -90.0
-180.0 NaN NaN NaN NaN -22.341 -21.57 -21.7346
-179.75 NaN NaN NaN NaN -22.3399 -21.5718 -21.7351
-179.5 NaN NaN NaN NaN -22.3389 -21.5736 -21.7356
-179.25 NaN NaN NaN NaN -22.3378 -21.5754 -21.736
⋮ ⋱ ⋮
178.75 NaN NaN NaN NaN -24.3424 -23.9036 -23.7343
179.0 NaN NaN NaN NaN -24.3419 -23.9043 -23.7341
179.25 NaN NaN NaN NaN -24.3415 -23.9049 -23.734
179.5 NaN NaN NaN NaN -24.341 -23.9056 -23.7339
179.75 NaN NaN NaN NaN … -24.3405 -23.9063 -23.7338WARNING
Note that you need to specify sampling=Intervals(Start()) for X and Y.
This requires that you run using Rasters.Lookups, where the Intervals and Start types are defined.
and take a look
fig, ax, plt = heatmap(ras_scratch)
Colorbar(fig[1,2], plt)
fig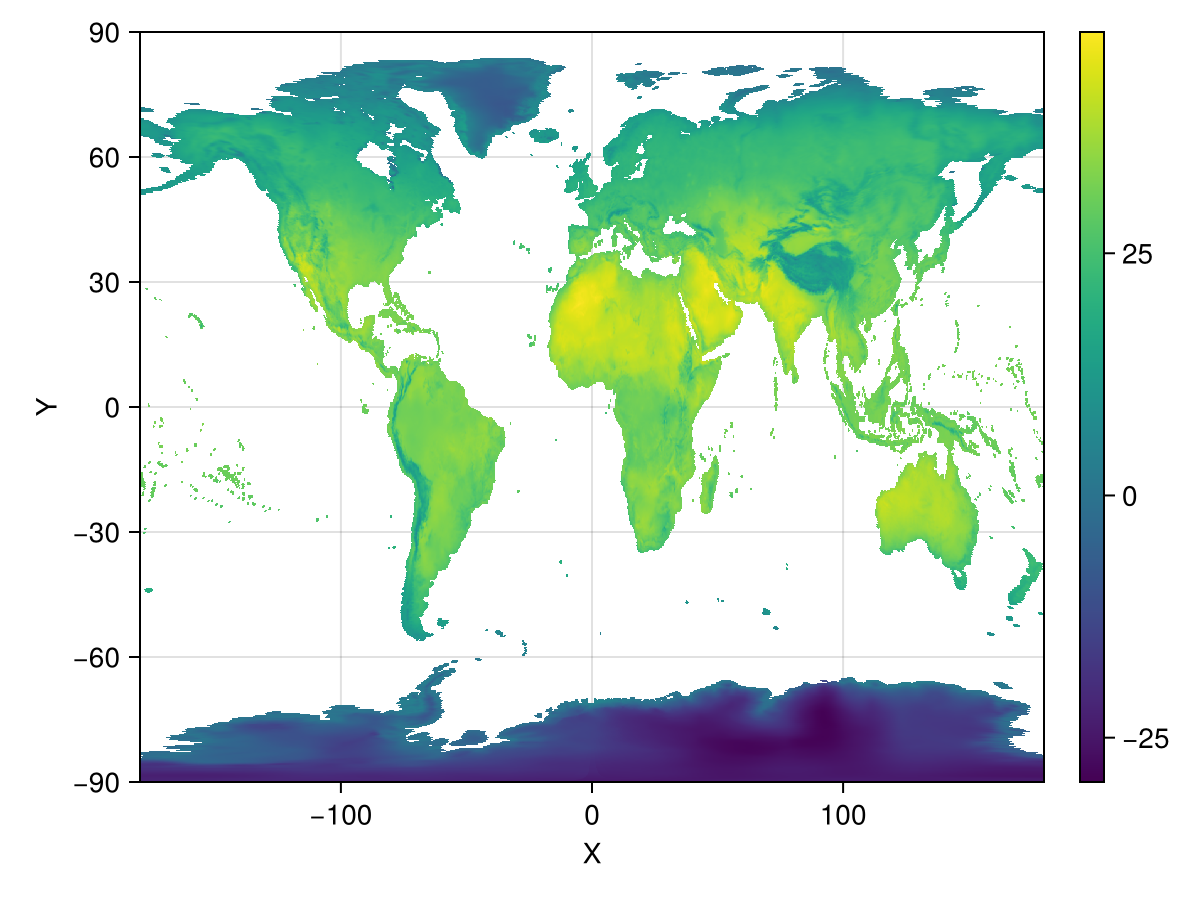
and the corresponding resampled projection
julia> ras_sin_s = resample(ras_scratch; size=(1440,720), crs=SINUSOIDAL_CRS, method="average")┌ 1440×720 Raster{Float64, 2} ┐
├─────────────────────────────┴────────────────────────────────────────── dims ┐
↓ X Projected{Float64} -2.0037508342789244e7:27820.552039794457:1.999626604247498e7 ForwardOrdered Regular Intervals{Start},
→ Y Projected{Float64} 9.974183816928538e6:-27781.912384183634:-1.0001011187299494e7 ReverseOrdered Regular Intervals{Start}
├──────────────────────────────────────────────────────────────────── metadata ┤
Metadata{Rasters.GDALsource} of Dict{String, Any} with 1 entry:
"filepath" => "/vsimem/tmp"
├────────────────────────────────────────────────────────────────────── raster ┤
extent: Extent(X = (-2.0037508342789244e7, 2.0024086594514776e7), Y = (-1.0001011187299494e7, 1.0001965729312722e7))
missingval: NaN
crs: +proj=sinu +lon_0=0 +type=crs
└──────────────────────────────────────────────────────────────────────────────┘
↓ → 9.97418e6 9.9464e6 9.91862e6 … -9.97323e6 -1.0001e7
-2.00375e7 NaN NaN NaN NaN NaN
-2.00097e7 NaN NaN NaN NaN NaN
⋮ ⋱ ⋮
1.99406e7 NaN NaN NaN NaN NaN
1.99684e7 NaN NaN NaN NaN NaN
1.99963e7 NaN NaN NaN … NaN NaNfig, ax, plt = heatmap(ras_sin_s)
Colorbar(fig[1,2], plt)
fig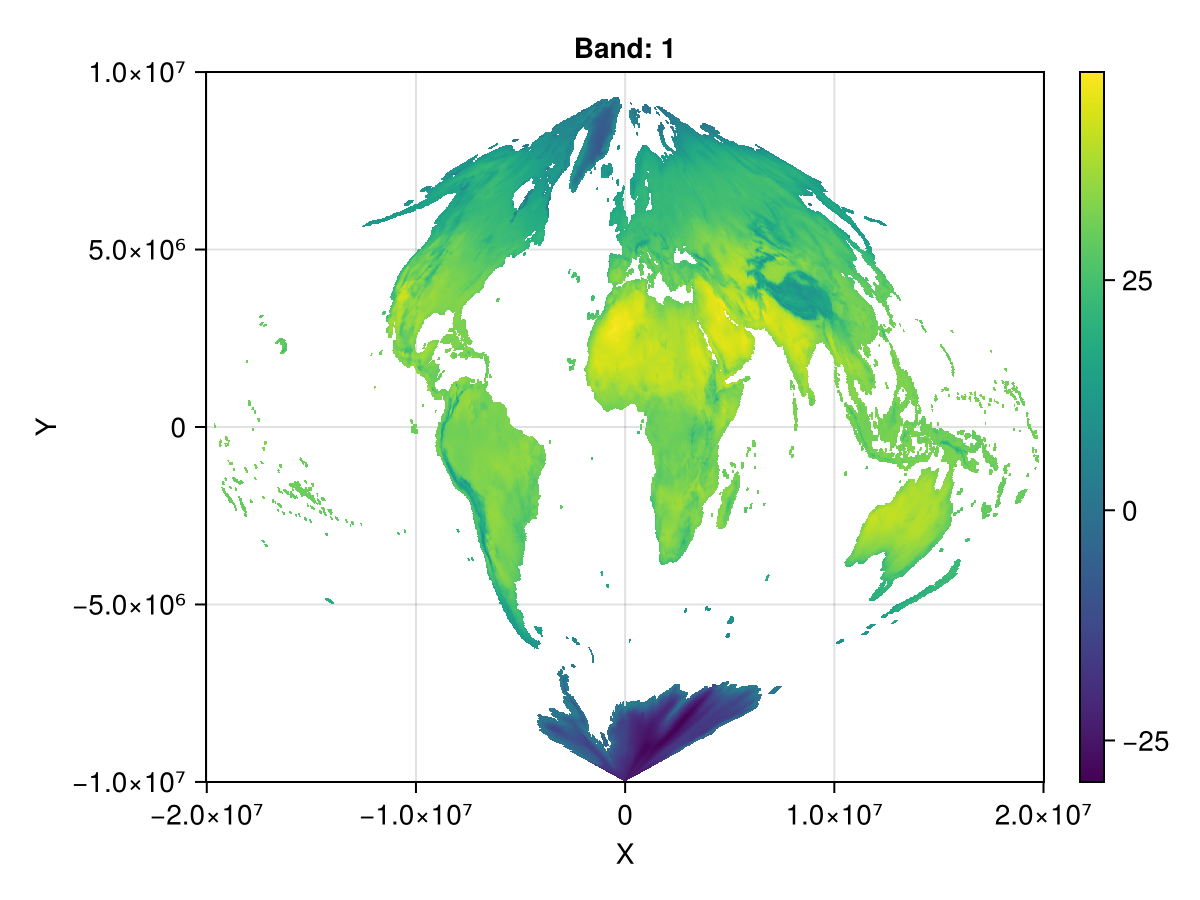
and go back from sin to epsg:
ras_epsg = resample(ras_sin_s; size=(1440,720), crs=EPSG(4326), method="average")
locus_resampled = DimensionalData.shiftlocus(Center(), ras_epsg)
fig, ax, plt = heatmap(locus_resampled)
Colorbar(fig[1,2], plt)
fig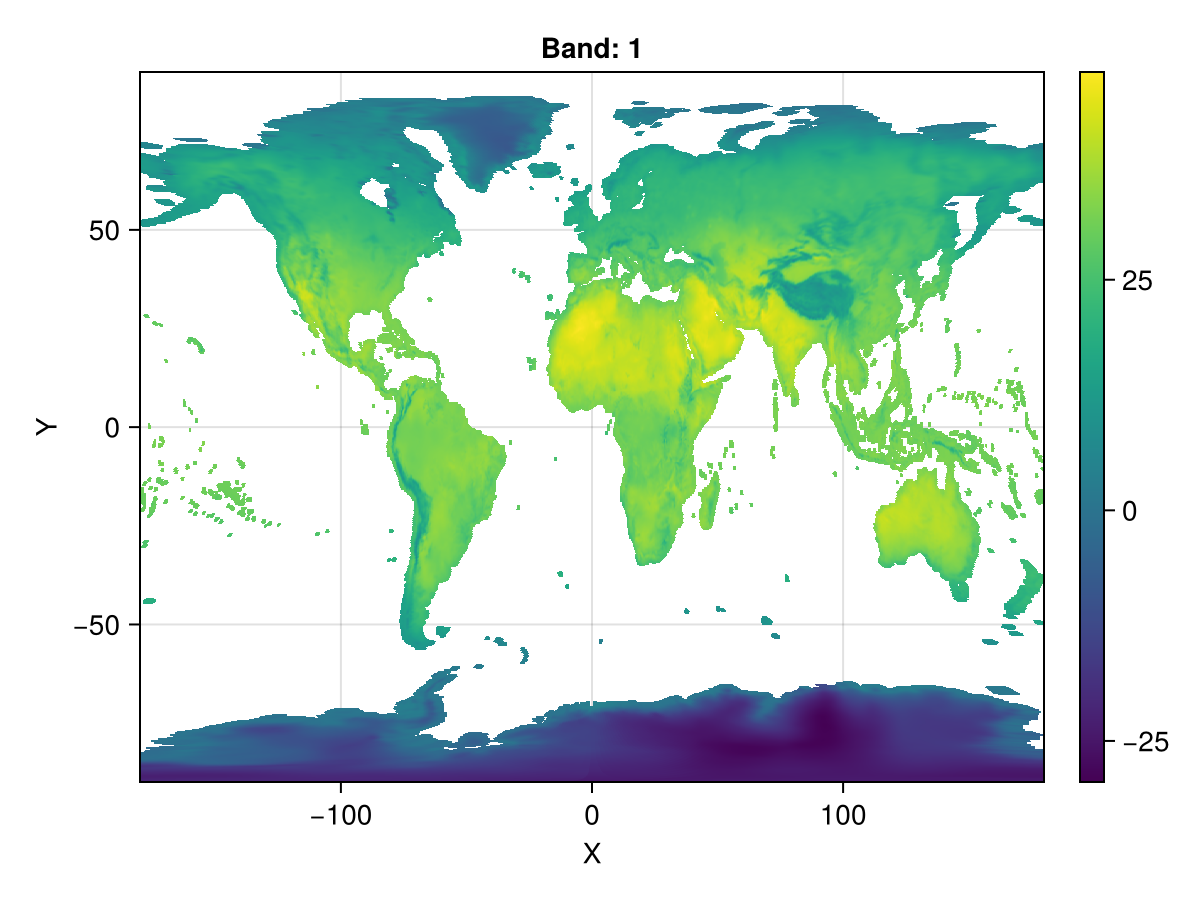
and compare the total counts again!
nansum(ras_sin_s), nansum(locus_resampled)(5.780817076729905e6, 6.287521031058559e6)DANGER
Note that all counts are a little bit off. Could we mitigate this some more?